<style> .reveal p{text-align:left;}</style> # 搜索 --- ## 1、搜索的概念 枚举算法：穷举所有的状态，进行判定，获得解。 然而有些问题的状态比较特殊，是由多个维度组成，比如百钱买百鸡，状态是公鸡数x、母鸡数y、小鸡数z的组合。如果维度不多，可以用多重循环实现，当维度比较多或者个数不确定的时候，就需要用到搜索算法了。 搜索算法利用递归函数来获得所有的维度组合，进而筛选出需要的状态，进行判定求解。 --- ## 2、搜索的要素 搜索算法往往采用递归函数的方式来实现搜索＋回溯 --- ### 2.1 退出 如果把搜索算法看成很多层选择的话，那么当每一层的选择（路径）都走完以后，就可以退出了。 --- ### 2.2 求解 最后一层有可行路径，表示有了一个解（从第一层到最后一层的路径）。 一般每一层有可行路径后，即进入下一层搜索，如果下一层超过了层数就表示有解。 --- ### 2.3 选择 每层根据可选的路径进行选择，根据某种判定条件检查路径是否可行，如果可行就进入下一层搜索。 如果所有选择都不可行（表示无解）则回退到上一层。 --- ### 2.4 回溯 当进入下一层前，记录本层的选择，一方面可能下一层的判定要用到，另一方面求解时用到。 当求解完成回退，或某层无解回退时，需要把上一层的记录清除，以便上一层再往下选择。 --- ## 3、案例 以1-3的全排列为例子，如下图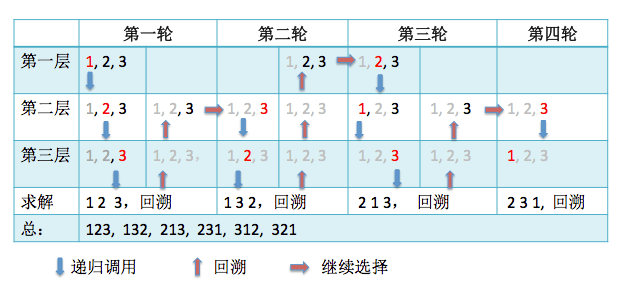：  --- * 第一轮： - 第一层1..3中选择了1 - 然后调用第二层1..3中选择了2（1已经被第一层选择） - 然后调用第三层1..3中选择了3（1，2已经被选） - 解为1 2 3，然后回溯到第三层 - 第三层已经没有可选，继续回溯到第二层 - 第二层还有3可以选择，因此作为第二轮的开始 * 第二轮： - 第一层不变，从第二轮开始 - 第二轮选择3 - 然后调用第三层1..3中选择2（1, 3已经被选） - 解为1 3 2，然后回溯到第三层 - 第三层已经没有可选，继续回溯到第二层 - 第二层已经没有可选，继续回溯到第一层 - 第一层还有2、3可选，因此作为第三轮的开始 * 第三轮 - ...依次类推 --- ## 4、常见分类及模型 ### 4.1 子集法和排列法 当所给问题是从n个元素的集合S中找出满足某种性质的子集时，可以使用子集法 当所给问题是从n个元素的集合S中找出满足某种性质的排列时，可以使用排列法 --- 子集法基本模型 ```c++ void search(int t) { //t 表示当前在第t层，即对集合 S 中的第 t 个元素进行判断 if (t > n){ //大于S中总的元素个数 ，遍历完成 处理解 返回 } for (int i = 0; i < = 1; i++) { to[t]=i;// 两种可能 加入(1)或者不加入(0)到解集合 search(t + 1); //对 t+1 层进行判断 } } ``` --- 排列法基本模型 ```c++ void search(int t) { //t 表示集合 S 的第 t 个元素 if (t > n){ 处理解 返回 } for(当前这层可行的选择){ 状态变化 search(t+1) 回溯 } } ``` --- ## 四、扩展理解 --- ### 1、解空间树 使用回溯法解题时，如果把每层搜索的状态按照树的结构连接起来，就会组成一个解空间树。树的一条边（从根到叶子）就是一个解，常见的解空间树一般可分为为排列树和子集树。 --- #### 1.1 排列树 当问题为寻求n个元素的某种排列时，解空间树称为排列树，排列树通常有n!个叶子节点（第一层有n个选择，第二层n-1，依次类推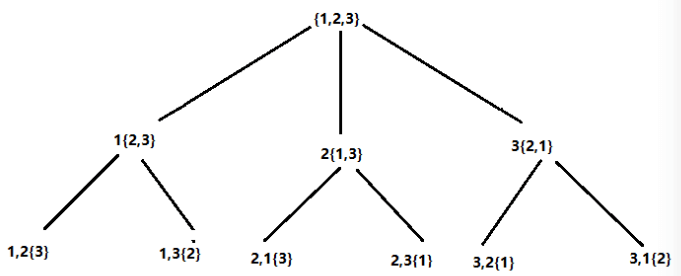）。  --- #### 1.2 子集树 当问题为在n个元素的集合种找某种子集时，解空间树称为子集树。子集树实际就是满二叉树，叶子节点为为2^n个。 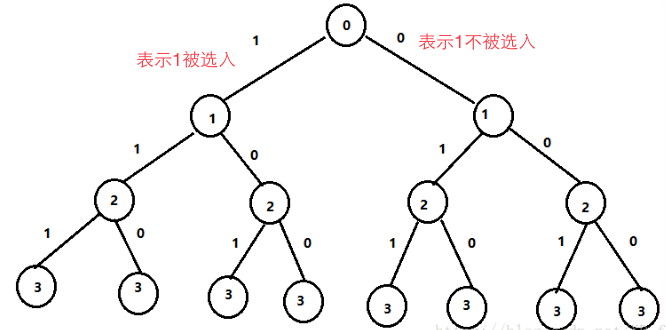 --- ## 五、例题与练习 --- #### 百钱百鸡问题 小明在学数学的时候碰到了百钱买百鸡的问题：现有100文钱，准备用来买公鸡、母鸡、小鸡共100只，其中公鸡一只5文、母鸡一只3文、小鸡三只1文，请问有哪几种购买方案（要把100文钱花光）。 编写程序，输出几种购买方案，用100文钱购买100只鸡。 > 正确答案： ``` 0 25 75 4 18 78 8 11 81 12 4 84 ``` #### 分析 --- #### 1-3排列(可重复)(搜索) ##### 题目: 从1-3里面选出三个数，可重复选择(第一个选了1，后面也能选),求出选择方案和总共有几种方案? > 输入格式：无输入 > 输出格式：选择方案，以及方案数 > 正确答案 > 1 1 1 > 1 1 2 > 1 1 3 > 1 2 1 > 1 2 2 > 1 2 3 > 1 3 1 > 1 3 2 > 1 3 3 > 2 1 1 > 2 1 2 > 2 1 3 > 2 2 1 > 2 2 2 > 2 2 3 > 2 3 1 > 2 3 2 > 2 3 3 > 3 1 1 > 3 1 2 > 3 1 3 > 3 2 1 > 3 2 2 > 3 2 3 > 3 3 1 > 3 3 2 > 3 3 3 > 27 --- ##### 分析 ###### 1、搜索的要素 解： 用t计算层数，当t>3时即表示一个解，此时可输出方案，计数递增。 每层选择的数，存储到a[]数组里，输出方案时使用。 状态：每层都循环1..3选择 回溯： t层数的清除：利用函数调用不会影响入参的机制，自动清除。 --- ###### 2、实现步骤 1. 数据定义与输入 2. 实现search(t)函数 3. 当t>3时，输出一个方案并计数 4. 循环本层的选择，可行就递归调用search(t+1) 5. main调用search函数，输出计数 --- ##### 代码： ```c++ #include<iostream> using namespace std; int a[5],cnt; void search(int t){ if(t>3){ cout<<a[1]<<" "<<a[2]<<" "<<a[3]; cout<<endl; cnt++; return; } for(int i=1;i<=3;i++){ a[t] = i; search(t+1); } } int main(){ search(1); cout << cnt; return 0; } ``` --- *问题:如果是1到n的全排列呢？* --- #### 练习： 砝码称重 [P356 砝码称重](/p/356) 有1g、2g、3g、5g、10g、20g（共六种类型）的砝码共若干枚（总重<=1000g），求用这些砝码能称出不同的重量数（不包括0）。 > 输入格式：每种砝码的最多个数 > 输出格式：Total=个数 > 输入格式： ``` 1 1 0 0 0 0 ``` 输出格式： ``` Total=3 ``` **本题预计获得60分左右。** --- #### 练习：1-3排列(可重复和为偶数)(搜索) ##### 题目描述 ``` 从1-3中选，排成三个数，求这三个数的和为偶数的排法及方案总数 ``` > 输入格式：无输入 > 输出格式：选择方案，以及方案数 ``` 正确答案 ``` 1 1 2 1 2 1 1 2 3 1 3 2 2 1 1 2 1 3 2 2 2 2 3 1 2 3 3 3 1 2 3 2 1 3 2 3 3 3 2 13 --- ##### 分析 --- ###### 1、搜索的要素 解： 用t计算层数，当t>3并且和为偶数时即表示一个解，此时可输出方案，计数递增。 每层选择的数，存储到a[]数组里，输出方案时使用。 状态：每层都循环1..3选择 回溯： t层数的清除：利用函数调用不会影响入参的机制，自动清除。 --- ##### 实验步骤 1. 数据定义与输入 2. 实现search(t，sum)函数 - 当t>m，sum为偶数时，输出一个方案并计数 - 循环本层的选择，可行就递归调用search(t+1) 3. main调用search函数，输出计数 ##### 实现代码： ```c++ ``` --- #### 练习：从N个中选出M个的排列 在1...n个元素中，选择出m个按照从小到大排序的元素，输出这些方案和方案数。 请使用排列法搜索。 输入样例 n和m： ``` 4 2 ``` 输出样例-前面都是方案，最后一行为方案数： ``` 1 2 1 3 1 4 2 3 2 4 3 4 6 ``` 输入样例2： ``` 5 3 ``` 输出样例2： ``` 1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5 10 ``` 数据范围： ``` 1<=m<=n<=10 ``` --- ##### 分析 ###### 1、思路 使用排列法进行搜索。 为了确保排序，我们可以每次选择的时候使用下界和上界进行控制： 下界：从已选的最后一个元素+1开始（保证比前面的大） 上界：给后面留足空间：n - (m-last-1) --- ###### 2、搜索 解：t>m表示已经选了m个元素： - 输出选择的a[] - 方案数递增 - 返回 --- **搜索:** 每次按上下界范围选择： - 选择范围：i=a[t-1]+1; i<=n-(m-t) - 保存：a[t] = i - 递归搜索 --- **回溯：** 参数自动回溯 ##### 三、实验步骤 1. 数据定义和输入 2. 实现search函数 3. main调用search(1)，输出方案数 --- 参考代码： : 此代码仅供参考。 ```c++ /* 输入n m， 输出 n选m的所有可能性 问题分层： 1. 层 表示什么 2. 有几层 3. 每层的可能性 4. 递归出口答案筛选 5. 能不能剪枝优化 5 2 1 2 1 3 1 4 1 5 2 3 2 4 2 5 3 4 3 5 4 5 */ #include<iostream> using namespace std; /* n选m: 第1个空 1 2 3 4 5 .... n 第2个空 ..... 第m个空 m+1 */ int a[1005]; bool to[1005]; int n, m; void show() { for(int i = 1; i <= m; i++) cout << a[i] << ' '; cout << endl; } /* 1 2 3 从小到大 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 */ bool check() { // a[1] < a[2] < a[3] ... < a[m] for(int i = 1; i < m; i++) if(a[i] > a[i + 1]) return false; return true; } /* 2 1 x x x check */ void search(int t) { // 第t个空 第t个被选出来的数 if(t > m){ if(check()) show(); return; } for(int i = 1; i <= n; i++){ if(to[i]) continue; a[t] = i; to[i] = true; search(t + 1); to[i] = false; } } int main() { cin >> n >> m; search(1); return 0; } ``` --- * [P789 全排列](http://39.99.183.126:8888/p/789) * 1317 [YBTJ1317 【例5.2】组合的输出](http://39.99.183.126:8888/p/YBTJ1317) * 1318 [YBTJ1318 【例5.3】自然数的拆分](http://39.99.183.126:8888/p/YBTJ1318) * 1212 [YBTJ1212 LETTERS](http://39.99.183.126:8888/p/YBTJ1212) * 1213 [YBTJ1213 八皇后问题](http://39.99.183.126:8888/p/YBTJ1213) * 1214 [YBTJ1214 八皇后](http://39.99.183.126:8888/p/YBTJ1214) * 1215 [YBTJ1215 迷宫](http://39.99.183.126:8888/p/YBTJ1215) * 1216 [YBTJ1216 红与黑](http://39.99.183.126:8888/p/YBTJ1216) * 1217 [YBTJ1217 棋盘问题](http://39.99.183.126:8888/p/YBTJ1217) * 1218 [YBTJ1218 取石子游戏](http://39.99.183.126:8888/p/YBTJ1218) * 1219 [YBTJ1219 马走日](http://39.99.183.126:8888/p/YBTJ1219) * 1220 [YBTJ1220 单词接龙](http://39.99.183.126:8888/p/YBTJ1220) * 1221 [YBTJ1221 分成互质组](http://39.99.183.126:8888/p/YBTJ1221)