入门级-数据结构-图的定义和存储

# 图

---

## 1、什么是图

![](https://cdn.itbegin.com//pics/admin/2018/11/c37c256672f14bee89618598750816e8.jpg)

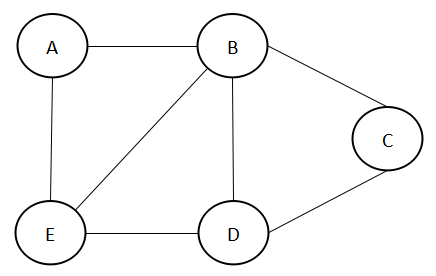以上就是一个图，包含5个顶点和7条边。简单的说，把点用边连起来，就叫做图。

---

`定义`：G = (V, E)

- G（graph）：表示一个图
- V（Vertext）：顶点（结点），非空有限集合
- E（Edge）：边的集合，可以为空

---

## 2、图的分类

### 2.1 无向图

如果图的边没有方向，称之为无向图。上面的例子就是一个无向图。

无向图的边（Edge），用(V1, V2)表示。

---

### 2.2 有向图

如果图的边有方向，称之为有向图，如下图：

![](https://cdn.itbegin.com//pics/admin/2018/11/e00e93f421004dc1a30827db4c12294b.jpg)

有向图的边用<V1, V2>，表示方向从V1到V2，也称为弧（Arc），V1为弧尾（Tail），V2为弧头（Head）。

---

### 2.3 加权图（网图）

如果一个图的边带有一个数值（通俗理解为边的“长度”，只是权可以为负数），就把这样的图称之为“加权图”，边上带有的数值称为“权”。

无向图带有权，称之为“无向加权图”，有向图带有权，称之为“有向加权图”。

![](https://cdn.itbegin.com//pics/admin/2018/11/51891df442ab4b21b661ecc7f0ec441d.jpg)

---

## 图的相关概念

----

## 相邻

在无向图 $G = (V, E)$ 中，若点 $v$ 是边 $e$ 的一个端点，则称 $v$ 和 $e$ 是 **关联的 $incident$** 或 **相邻的 $adjacent$**。对于两顶点 $u$ 和 $v$，若存在边 $(u, v)$，则称 $u$ 和 $v$ 是 **相邻的 $adjacent$**。

一个顶点 $v \in V$ 的 **邻域 $neighborhood$** 是所有与之相邻的顶点所构成的集合，记作 $N(v)$。

一个点集 $S$ 的邻域是所有与 $S$ 中至少一个点相邻的点所构成的集合，记作 $N(S)$，即：

$$
N(S) = \bigcup_{v \in S} N(v)
$$

----

## 简单图

$\color{blue}{自环 (loop)}$：对 $E$ 中的边 $e = (u, v)$，若 $u = v$，则 $e$ 被称作一个自环。

$\color{blue}{重边 (multiple edge)}$：若 $E$ 中存在两个完全相同的元素（边）$e_1, e_2$，则它们被称作（一组）重边。

----

### 简单图 (simple graph)：

若一个图中没有自环和重边，它被称为简单图。

具有至少两个顶点的简单无向图中一定存在度相同的结点。（[鸽巢原理](../math/combinatorics/drawer-principle.md)）

如果一张图中有自环或重边，则称它为  多重图 (multigraph) 。

### warning

在无向图中 $(u, v)$ 和 $(v, u)$ 算一组重边，而在有向图中，$u \to v$ 和 $v \to u$ 不为重边。

### warning

在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。

----

## 度数

与一个顶点 $v$ 关联的边的条数称作该顶点的 **度 $degree$**，记作 $d(v)$。特别地，对于边 $(v, v)$，则每条这样的边要对 $d(v)$ 产生 $2$ 的贡献。

对于无向简单图，有 $d(v) = \left| N(v) \right|$。

----

握手定理（又称图论基本定理）：对于任何无向图 $G = (V, E)$，有 $\sum_{v \in V} d(v) = 2 \left| E \right|$。

----

推论：在任意图中，度数为奇数的点必然有偶数个。

若 $d(v) = 0$，则称 $v$ 为 **孤立点 $isolated vertex$**。

若 $d(v) = 1$，则称 $v$ 为 **叶节点 $leaf vertex$**/**悬挂点 $pendant vertex$**。

若 $2 \mid d(v)$，则称 $v$ 为 **偶点 $even vertex$**。

若 $2 \nmid d(v)$，则称 $v$ 为 **奇点 $odd vertex$**。图中奇点的个数是偶数。

若 $d(v) = \left| V \right| - 1$，则称 $v$ 为 **支配点 $universal vertex$**。

----

对一张图，所有节点的度数的最小值称为 $G$ 的 **最小度 $minimum degree$**，记作 $\delta (G)$；最大值称为 **最大度 $maximum degree$**，记作 $\Delta (G)$。即：$\delta (G) = \min_{v \in G} d(v)$，$\Delta (G) = \max_{v \in G} d(v)$。

在有向图 $G = (V, E)$ 中，以一个顶点 $v$ 为起点的边的条数称为该顶点的 **出度 $out-degree$**，记作 $d^+(v)$。以一个顶点 $v$ 为终点的边的条数称为该节点的 **入度 $in-degree$**，记作 $d^-(v)$。显然 $d^+(v)+d^-(v)=d(v)$。

----

对于任何有向图 $G = (V, E)$，有：

$$
\sum_{v \in V} d^+(v) = \sum_{v \in V} d^-(v) = \left| E \right|
$$

若对一张无向图 $G = (V, E)$，每个顶点的度数都是一个固定的常数 $k$，则称 $G$ 为 **$k$- 正则图 $$k$-regular graph$**。

如果给定一个序列 a，可以找到一个图 G，以其为度数列，则称 a 是 **可图化** 的。

如果给定一个序列 a，可以找到一个简单图 G，以其为度数列，则称 a 是 **可简单图化** 的。

----

## 路径

**途径 $walk$**：途径是连接一连串顶点的边的序列，可以为有限或无限长度。形式化地说，一条有限途径 $w$ 是一个边的序列 $e_1, e_2, \ldots, e_k$，使得存在一个顶点序列 $v_0, v_1, \ldots, v_k$ 满足 $e_i = (v_{i-1}, v_i)$，其中 $i \in [1, k]$。这样的途径可以简写为 $v_0 \to v_1 \to v_2 \to \cdots \to v_k$。通常来说，边的数量 $k$ 被称作这条途径的 **长度**（如果边是带权的，长度通常指途径上的边权之和，题目中也可能另有定义）。

**迹 $trail$**：对于一条途径 $w$，若 $e_1, e_2, \ldots, e_k$ 两两互不相同，则称 $w$ 是一条迹。

**路径 $path$**（又称 **简单路径 $simple path$**）：对于一条迹 $w$，若其连接的点的序列中点两两不同，则称 $w$ 是一条路径。

**回路 $circuit$**：对于一条迹 $w$，若 $v_0 = v_k$，则称 $w$ 是一条回路。

**环/圈 $cycle$**（又称 **简单回路/简单环 $simple circuit$**）：对于一条回路 $w$，若 $v_0 = v_k$ 是点序列中唯一重复出现的点对，则称 $w$ 是一个环。

----

### warning
关于路径的定义在不同地方可能有所不同，如，「路径」可能指本文中的「途径」，「环」可能指本文中的「回路」。如果在题目中看到类似的词汇，且没有「简单路径」/「非简单路径」（即本文中的「途径」）等特殊说明，最好询问一下具体指什么。

----

## 子图

对一张图 $G = (V, E)$，若存在另一张图 $H = (V', E')$ 满足 $V' \subseteq V$ 且 $E' \subseteq E$，则称 $H$ 是 $G$ 的 **子图 $subgraph$**，记作 $H \subseteq G$。

若对 $H \subseteq G$，满足 $\forall u, v \in V'$，只要 $(u, v) \in E$，均有 $(u, v) \in E'$，则称 $H$ 是 $G$ 的 **导出子图/诱导子图 $induced subgraph$**。

容易发现，一个图的导出子图仅由子图的点集决定，因此点集为 $V'$($V' \subseteq V$) 的导出子图称为 $V'$ 导出的子图，记作 $G \left[ V' \right]$。

若 $H \subseteq G$ 满足 $V' = V$，则称 $H$ 为 $G$ 的 **生成子图/支撑子图 $spanning subgraph$**。

显然，$G$ 是自身的子图，支撑子图，导出子图；[无边图](#特殊的图) 是 $G$ 的支撑子图。原图 $G$ 和无边图都是 $G$ 的平凡子图。

如果一张无向图 $G$ 的某个生成子图 $F$ 为 $k$- 正则图，则称 $F$ 为 $G$ 的一个 **$k$- 因子 $$k$-factor$**。

如果有向图 $G = (V, E)$ 的导出子图 $H = G \left[ V^\ast \right]$ 满足 $\forall v \in V^\ast, (v, u) \in E$，有 $u \in V^\ast$，则称 $H$ 为 $G$ 的一个 **闭合子图 $closed subgraph$**。
----

## 稀疏图/稠密图

若一张图的边数远小于其点数的平方，那么它是一张 **稀疏图 $sparse graph$**。

若一张图的边数接近其点数的平方，那么它是一张 **稠密图 $dense graph$**。

这两个概念并没有严格的定义，一般用于讨论 [时间复杂度](../basic/complexity.md) 为 $O(|V|^2)$ 的算法与 $O(|E|)$ 的算法的效率差异（在稠密图上这两种算法效率相当，而在稀疏图上 $O(|E|)$ 的算法效率明显更高）。

---

## 3、邻接矩阵

图的顶点可用一个一维数组来存储，如果只有编号的话一般都默认1到n即可。

图的边一般使用邻接矩阵或邻接表来存储，特殊情况下也可以使用边的数组来存储。

大部分情况下，noi算法题都使用邻接矩阵来表示图，因此我们这里先学习邻接矩阵。

---

### 3.1 邻接矩阵

使用二维数组来存储图中所有边，a[x][y]的值表示一条边（x, y）或<x, y>的信息。

---

例如对于本例的无向图：

![](https://cdn.itbegin.com//pics/admin/2018/11/c37c256672f14bee89618598750816e8.jpg)

---

其邻接矩阵如下：

|0|1|0|0|1|
|-|-:|-:|-:|-:|
|1|0|1|1|1|
|0|1|0|1|0|
|0|1|1|0|1|
|1|1|0|1|0|

---

以上1表示连接，0表示无连接，行列下标分别表示A、B、C、D、E顶点。

`对称性`：无向图的邻接矩阵是对称的，既a[x][y] = a[y][x]。

---

### 3.2 有向图的邻接矩阵

对有向图来说，邻接矩阵也是适用的，只是不对称。

![](https://cdn.itbegin.com//pics/admin/2018/11/e00e93f421004dc1a30827db4c12294b.jpg)

---

其邻接矩阵如下：

|0|1|0|0|1|
|-|-|-|-|-|
|0|0|1|1|0|
|0|0|0|1|0|
|0|0|0|0|1|
|0|1|0|0|0|

---

### 3.3 加权图的邻接矩阵

对加权图来说，邻接矩阵的值就不能只是1或0了，需要存储边的权。

![](https://cdn.itbegin.com//pics/admin/2018/11/51891df442ab4b21b661ecc7f0ec441d.jpg)

---

有向加权图的邻接矩阵如下：

|0|2|0|0|2|
|-|-|-|-|-|
|0|0|4|4|0|
|0|0|0|6|0|
|0|0|0|0|8|
|0|10|0|0|0|

`注意`：为了避免有权的值是0，有时候需要将"无连接的边"设计为不会出现的数值，例如无穷大。

---

## 4、图的输入

如果用邻接矩阵来表示一个图，就需要将输入的信息转化为邻接矩阵，俗称“建边”。

如果一个试题输入就是一个邻接矩阵，显然就直接读取就好。

有时候，一个试题会输入点和边的数目n、m，然后输入m行，每行用两个点x、y表示边(x, y)。

---

例如-第一行n和m，接下来m行都是边：

```
5 5
1 2
2 3
2 4
3 4
4 5
```

---

这种情况，就需要根据边(x, y)进行建边：

```
int n, m, x, y;
cin>>n>>m;
for(int i=1; i<=m; i++)
  cin>>x>>y;
  g[x][y] = g[y][x] = 1; //对称
```

`注意`：

* 如果是有向图，则不需要考虑对称。
* 如果是权图，则每行输入三个数，表示权为z的边(x, y) 。

---

## 扩展理解

#### 1、图的表示

如何表示一个图？

* 图形
* 点集与边集
* 邻接矩阵
* 邻接表
* 关联矩阵

---

第一个是肉眼能显然理解的图形，后面都是代码里存储的数据。

我们需要习惯在图形与数据之间切换，做到对着数据能轻松看懂对应图的结构，这样对学习图论就会很有帮助。

![](https://cdn.itbegin.com//pics/admin/2018/11/e00e93f421004dc1a30827db4c12294b.jpg)

---

`上图的输入`：

```
5 7
A B C D E
1 2
1 5
2 3
2 4
3 4
4 5
5 2
```

---

`邻接矩阵内容`：

|0|1|0|0|1|
|-|-|-|-|-|
|0|0|1|1|0|
|0|0|0|1|0|
|0|0|0|0|1|
|0|1|0|0|0|

---

`邻接表内容`：

|顶点|边1| 边 2| .....|
|---|---|--------|--|
|A|2    | 5|
|B|3    | 4|
|C|4|
|D|5|
|E|2|

---

#### 2、邻接矩阵与桶数组

如果学过桶数组，就会比较容易理解邻接矩阵。

第i行是一个数组，表示编号i的顶点，所连接的边，使用了桶数组来存储。

下标i和j表示图中任意两个点，g[i][j]的值用来规定两个点连接的信息，例如：

* true表示连接、false表示不连接
* 数值表示边上的权，inf表示不连接
* ......

---

## 5、邻接表

用邻接矩阵来表示图，需要用到二维数组，其中很多没有连接的边也都需要占位，占内存比较大，运算复杂度也高。

另外一种方式就是使用邻接表，只存储每个顶点连接的边（边的个数不定）。这样对于大的稀疏图就可以节约大量的内存，同时访问起来更加快速。

---

邻接表核心结构：

* 顶点用一维数组存储
* 每个顶点的所有邻接边构成一个长度不定的线性表

由于邻接边的动态特性，一般可使用结构体＋指针（单向链表）的方式来实现邻接表，但如果对链表知识没有掌握的同学，也可以采用其它方法实现动态线性表，例如Vector、链式前向星等。

---

## 6、邻接表案例

![](https://cdn.itbegin.com//pics/admin/2018/11/e00e93f421004dc1a30827db4c12294b.jpg)

---

邻接表内容：

|顶点|边1| 边 2| .....|
|---|---|--------|--|
|A|2    | 5|
|B|3    | 4|
|C|4|
|D|5|
|E|2|

---

## 7、Vector实现

Vector是c++ stl库提供的可变大小的序列容器，基本操作：

* 头文件：`#include <vector>`
* 声明变量：`vector<int> vec`
* 增加元素：`vec.push_back(a)`
* 下标访问：`vec[i]，从0开始到vec.size()-1`

可变大小的特性用来实现邻接表非常合适:

`注`：可理解成动态长度的数组。

---

### 7.1 邻接表定义

```c
vector<int> g[N];//用vector存储每个顶点连接的边
```

如果加权图，可用一个结构体，例如：

```c++
struct Edge {
  int y; //边连接的顶点
  int w; //权
};
vector<Edge> g[N];
```

也可用边数组Edge e[M]存储每条边，然后g[x]里存放边的序号（数组下标），例如：

---

### 7.2 建边

直接在vector里存边：

```c++
cin>>x>>y; //输入一条边
g[x].push_back(y);  //新增一条边
//加权图增加结构体：
g[x].push_back((Edge){y, w}); 
//无向图一条边加两次：
g[y].push_back(x);
```

---

或vector里存边的序号：

```c
cin>>x>>y;
e[i] = (Edge) {x, y}
g[x].push_back(i);
```

---

### 7.3 遍历

```c
for(int j=0; j<g[i].size();  j++)
  访问 g[i][j];
```

---

## 8、指针单链表实现

把同一个顶点连接的所有边以单链表的方式连接起来，访问的时候按照next元素循环读取。

常见的实现是用结构体＋指针实现单链表。

相比较vector的实现，单链表理解起来要晦涩一些，因此我们建议用vector方式更好，当然如果是超大图存在内存与时间要求的，使用单链表会有性能的优势。

---

### 8.1 邻接表定义

```
struct Edge {
  int end;
  Edge *next;
};
Edge* g[N];
```

---

### 8.2 建边

```
Edge* e = new Edge;
      e->end = y[i];
      e->next = g[x[i]];
      g[x[i]] = e;
    }
```

以上主要是把新的边作为第一条边，其next指向旧的第一条边。

---

### 8.3 遍历

```
for(Edge* e=g[i]; e!=NULL; e=e->next)
      //访问e
```

---

## 9、链式前向星实现

这是用静态数组实现单链表的一种技巧，将每个边用结构体的形态存储成一个边集（数组），每个边的next指向同一起点的下一条边在边集里的的序号，事实上就是一个链表。

g[N]为邻接表，存储每个顶点连接的第一条边（在边集里的序号）。

---

### 9.1 定义

```
struct Edge {
  int end;//终点
  int next;//下一条边的序号，0表示没有
};
Edge e[M];//边数组，其下标做为边的编号
int g[N];//邻接表，存储第一个edge
```

---

### 9.2 建边

```
e[i].end = y[i];
    e[i].next = g[x[i]];
    g[x[i]] = i;
```

---

### 9.2 遍历

```
for(int j=g[i]; j>0; j=e[j].next)
      //访问e[j]
```

---

## 扩展理解

#### 1、结构体

结构体将多个字段聚合成一个类型，用struct关键字定义：

```
struct Person {
  string name;
  int age;
};

Person p1, p2, p3;
```

---

`注意`：以上是c++语法，在c语言中，变量声明前要加struct。

---

#### 2、访问成员

结构体变量的成员，通过.来访问，例如：

```
Person p1;
p1.age = 20;
```

如果是指针变量，则通过->来访问，例如：

```
Person *p1 = new Person;
p1->age = 20;
```

---

#### 3、指针释放

对于new出来的指针，需要显示调用delete进行释放，否则会内存泄露。

```
Person *p1 = new Person;
delete p1;
```

---

#### 4、反图

有时候，需要存储一个图的反图：

```
g1[x].push_back(y);//正图
g2[y].push_back(x);//反图
```
---

## 例题与练习
|题目|
|---|
|[小A的烦恼](http://39.99.183.126:8888/p/CCFPB06D05)|
|[Martial artist](http://39.99.183.126:8888/p/abc226c)|
|[Triangle (Easier)](http://39.99.183.126:8888/p/abc262b)|
|[Adjacency List](http://39.99.183.126:8888/p/abc276b)|
|[FF](http://39.99.183.126:8888/p/abc278c)|