提高级-图论算法-最小生成树

# 最小生成树

---

## 定义

我们定义无向连通图的 **最小生成树**（Minimum Spanning Tree，MST）为边权和最小的生成树。

注意：只有连通图才有生成树，而对于非连通图，只存在生成森林。

---

## Kruskal 算法

Kruskal 算法是一种常见并且好写的最小生成树算法，由 Kruskal 发明。该算法的基本思想是从小到大加入边，是个贪心算法。

### 前置知识

[并查集](../ds/dsu.md)、[贪心](../basic/greedy.md)、[图的存储](./save.md)。

---

### 实现

图示：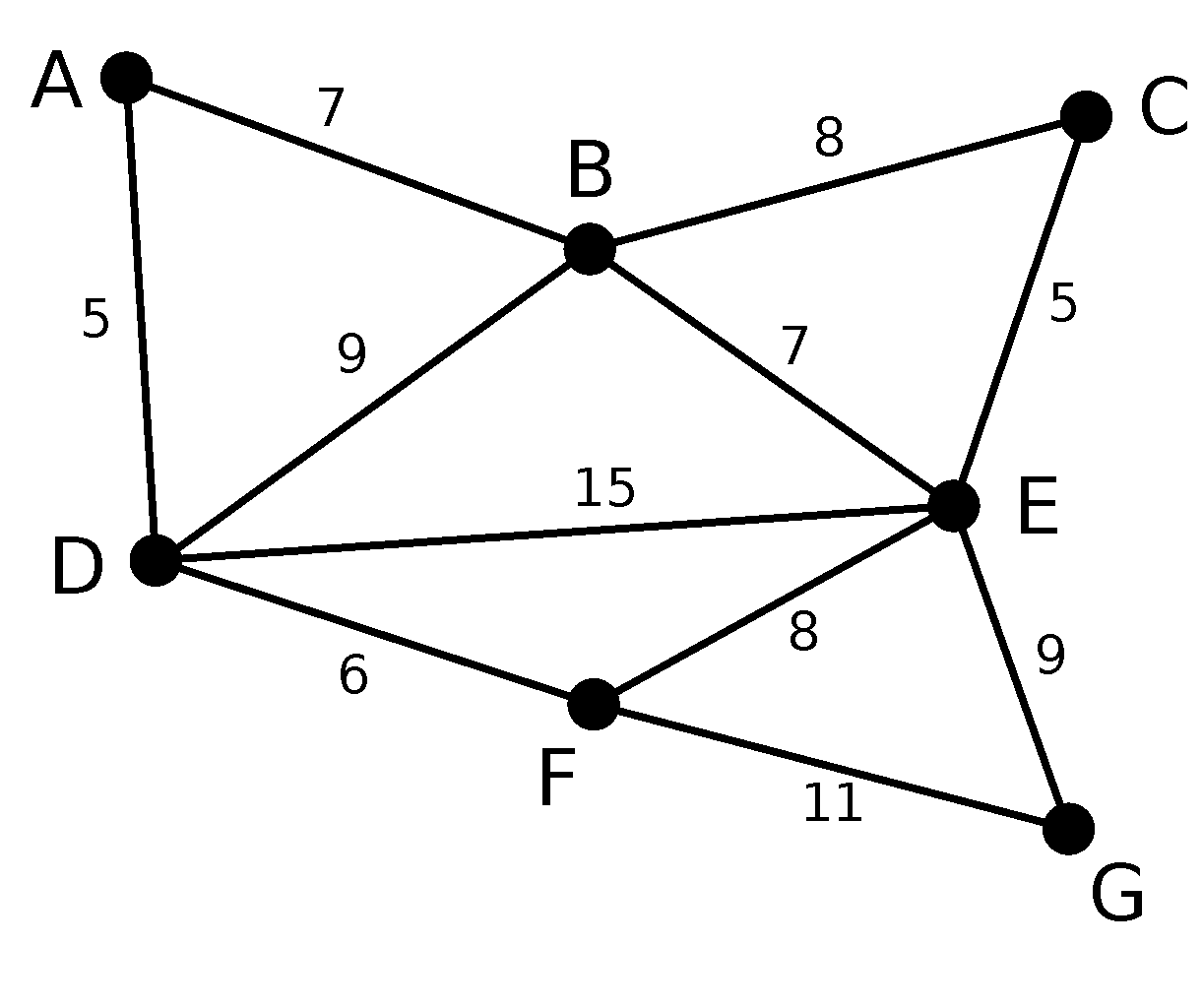

![](http://39.99.183.126:8888/file/2/mst-2.apng)

---

伪代码：
$$
\begin{array}{ll}
1 &  \textbf{Input. } \text{The edges of the graph } e , \text{ where each element in } e \text{ is } (u, v, w) \\\\
  &  \text{ denoting that there is an edge between } u \text{ and } v \text{ weighted } w . \\\\
2 &  \textbf{Output. } \text{The edges of the MST of the input graph}.\\\\
3 &  \textbf{Method. } \\\\
4 &  result \gets \varnothing \\\\
5 &  \text{sort } e \text{ into nondecreasing order by weight } w \\\\
6 &  \textbf{for} \text{ each } (u, v, w) \text{ in the sorted } e \\\\
7 &  \qquad \textbf{if } u \text{ and } v \text{ are not connected in the union-find set } \\\\
8 &  \qquad\qquad \text{connect } u \text{ and } v \text{ in the union-find set} \\\\
9 &  \qquad\qquad  result \gets result\;\bigcup\ \{(u, v, w)\} \\\\
10 &  \textbf{return }  result
\end{array}
$$

---

算法虽简单，但需要相应的数据结构来支持……具体来说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。

抽象一点地说，维护一堆 **集合**，查询两个元素是否属于同一集合，合并两个集合。

其中，查询两点是否连通和连接两点可以使用并查集维护。

如果使用 $O(m\log m)$ 的排序算法，并且使用 $O(m\alpha(m, n))$ 或 $O(m\log n)$ 的并查集，就可以得到时间复杂度为 $O(m\log m)$ 的 Kruskal 算法。

---

### 证明

思路很简单，为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 $n-1$ 条边，即形成了一棵树。

证明：使用归纳法，证明任何时候 K 算法选择的边集都被某棵 MST 所包含。

基础：对于算法刚开始时，显然成立（最小生成树存在）。

归纳：假设某时刻成立，当前边集为 $F$，令 $T$ 为这棵 MST，考虑下一条加入的边 $e$。

---

如果 $e$ 属于 $T$，那么成立。

否则，$T+e$ 一定存在一个环，考虑这个环上不属于 $F$ 的另一条边 $f$（一定只有一条）。

首先，$f$ 的权值一定不会比 $e$ 小，不然 $f$ 会在 $e$ 之前被选取。

然后，$f$ 的权值一定不会比 $e$ 大，不然 $T+e-f$ 就是一棵比 $T$ 还优的生成树了。

所以，$T+e-f$ 包含了 $F$，并且也是一棵最小生成树，归纳成立。

---

## Prim 算法

Prim 算法是另一种常见并且好写的最小生成树算法。该算法的基本思想是从一个结点开始，不断加点（而不是 Kruskal 算法的加边）。

---

### 实现

图示：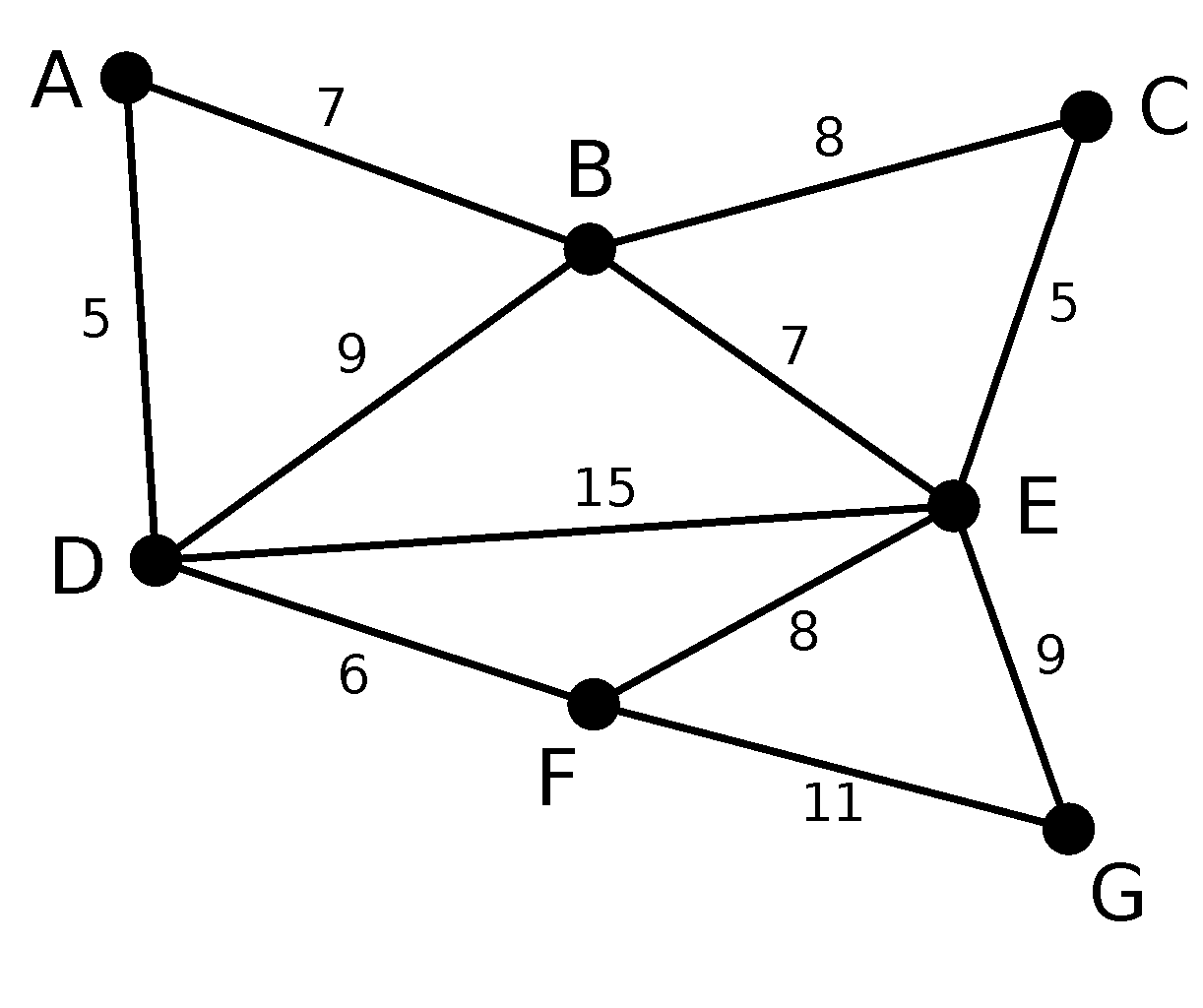

![](http://39.99.183.126:8888/file/2/mst-3.apng)

---

具体来说，每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

其实跟 Dijkstra 算法一样，每次找到距离最小的一个点，可以暴力找也可以用堆维护。

堆优化的方式类似 Dijkstra 的堆优化，但如果使用二叉堆等不支持 $O(1)$ decrease-key 的堆，复杂度就不优于 Kruskal，常数也比 Kruskal 大。所以，一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，暴力 Prim 的复杂度比 Kruskal 优，但 **不一定** 实际跑得更快。

暴力：$O(n^2+m)$。

二叉堆：$O((n+m) \log n)$。

Fib 堆：$O(n \log n + m)$。

---

伪代码：

$$
\begin{array}{ll}
1 &  \textbf{Input. } \text{The nodes of the graph }V\text{ ; the function }g(u, v)\text{ which}\\\\
  &  \text{means the weight of the edge }(u, v)\text{; the function }adj(v)\text{ which}\\\\
  &  \text{means the nodes adjacent to }v.\\\\
2 &  \textbf{Output. } \text{The sum of weights of the MST of the input graph.} \\\\
3 &  \textbf{Method.} \\\\
4 &  result \gets 0 \\\\
5 & \text{choose an arbitrary node in }V\text{ to be the }root \\\\
6 &  dis(root)\gets 0 \\\\
7 &  \textbf{for } \text{each node }v\in(V-\{root\}) \\\\
8 &  \qquad  dis(v)\gets\infty \\\\
\end{array}
$$

---

$$
\begin{array}{ll}
9 &  rest\gets V \\\\
10 &  \textbf{while }  rest\ne\varnothing \\\\
11 &  \qquad cur\gets \text{the node with the minimum }dis\text{ in }rest \\\\
12 &  \qquad  result\gets result+dis(cur) \\\\
13 &  \qquad  rest\gets rest-\{cur\} \\\\
14 &  \qquad  \textbf{for}\text{ each node }v\in adj(cur) \\\\
15 &  \qquad\qquad  dis(v)\gets\min(dis(v), g(cur, v)) \\\\
16 &  \textbf{return }  result 
\end{array}
$$
---
注意：上述代码只是求出了最小生成树的权值，如果要输出方案还需要记录每个点的 $dis$ 代表的是哪条边。

---

"代码实现"
```cpp
// 使用二叉堆优化的 Prim 算法。
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int N = 5050, M = 2e5 + 10;

struct E {
  int v, w, x;
} e[M * 2];

int n, m, h[N], cnte;

void adde(int u, int v, int w) { e[++cnte] = E{v, w, h[u]}, h[u] = cnte; }

struct S {
  int u, d;
};

bool operator<(const S &x, const S &y) { return x.d > y.d; }

priority_queue<S> q;
int dis[N];
bool vis[N];

int res = 0, cnt = 0;

void Prim() {
  memset(dis, 0x3f, sizeof(dis));
  dis[1] = 0;
  q.push({1, 0});
  while (!q.empty()) {
    if (cnt >= n) break;
    int u = q.top().u, d = q.top().d;
    q.pop();
    if (vis[u]) continue;
    vis[u] = 1;
    ++cnt;
    res += d;
    for (int i = h[u]; i; i = e[i].x) {
      int v = e[i].v, w = e[i].w;
      if (w < dis[v]) {
        dis[v] = w, q.push({v, w});
      }
    }
  }
}

int main() {
  cin >> n >> m;
  for (int i = 1, u, v, w; i <= m; ++i) {
    cin >> u >> v >> w, adde(u, v, w), adde(v, u, w);
  }
  Prim();
  if (cnt == n)
    cout << res;
  else
    cout << "No MST.";
  return 0;
}
```

---

### 证明

从任意一个结点开始，将结点分成两类：已加入的，未加入的。

每次从未加入的结点中，找一个与已加入的结点之间边权最小值最小的结点。

然后将这个结点加入，并连上那条边权最小的边。

重复 $n-1$ 次即可。

---

证明：还是说明在每一步，都存在一棵最小生成树包含已选边集。

基础：只有一个结点的时候，显然成立。

归纳：如果某一步成立，当前边集为 $F$，属于 $T$ 这棵 MST，接下来要加入边 $e$。

如果 $e$ 属于 $T$，那么成立。

否则考虑 $T+e$ 中环上另一条可以加入当前边集的边 $f$。

首先，$f$ 的权值一定不小于 $e$ 的权值，否则就会选择 $f$ 而不是 $e$ 了。

然后，$f$ 的权值一定不大于 $e$ 的权值，否则 $T+e-f$ 就是一棵更小的生成树了。

因此，$e$ 和 $f$ 的权值相等，$T+e-f$ 也是一棵最小生成树，且包含了 $F$。

---

## Boruvka 算法

接下来介绍另一种求解最小生成树的算法——Boruvka 算法。该算法的思想是前两种算法的结合。它可以用于求解无向图的最小生成森林。（无向连通图就是最小生成树。）

在边具有较多特殊性质的问题中，Boruvka 算法具有优势。例如 [CF888G](https://codeforces.com/problemset/problem/888/G) 的完全图问题。

---

为了描述该算法，我们需要引入一些定义：

1.  定义 $E'$ 为我们当前找到的最小生成森林的边。在算法执行过程中，我们逐步向 $E'$ 加边，定义 **连通块** 表示一个点集 $V'\subseteq V$，且这个点集中的任意两个点 $u$，$v$ 在 $E'$ 中的边构成的子图上是连通的（互相可达）。
2.  定义一个连通块的 **最小边** 为它连向其它连通块的边中权值最小的那一条。

初始时，$E'=\varnothing$，每个点各自是一个连通块：

1.  计算每个点分别属于哪个连通块。将每个连通块都设为「没有最小边」。
2.  遍历每条边 $(u, v)$，如果 $u$ 和 $v$ 不在同一个连通块，就用这条边的边权分别更新 $u$ 和 $v$ 所在连通块的最小边。
3.  如果所有连通块都没有最小边，退出程序，此时的 $E'$ 就是原图最小生成森林的边集。否则，将每个有最小边的连通块的最小边加入 $E'$，返回第一步。

---

下面通过一张动态图来举一个例子（图源自 [维基百科](https://en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm)）：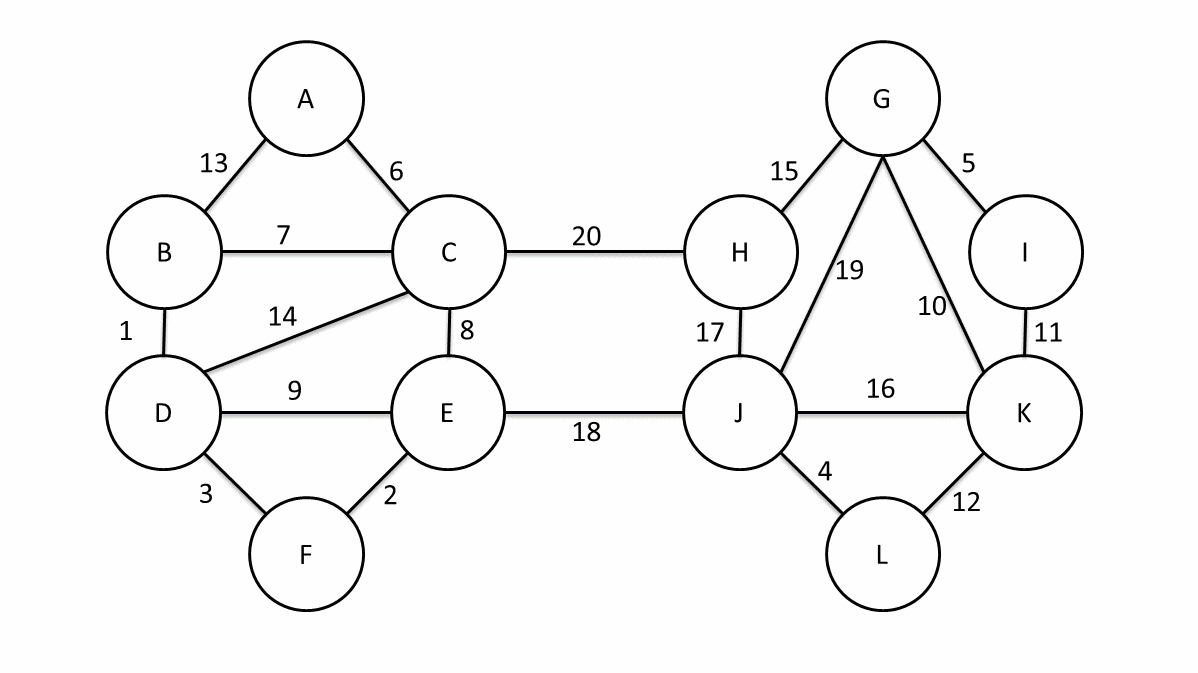

![eg](http://39.99.183.126:8888/file/2/mst-1.apng)

---

当原图连通时，每次迭代连通块数量至少减半，算法只会迭代不超过 $O(\log V)$ 次，而原图不连通时相当于多个子问题，因此算法复杂度是 $O(E\log V)$ 的。给出算法的伪代码：（修改自 [维基百科](https://en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm)）

---

$$
\begin{array}{ll}
1 &  \textbf{Input. } \text{A graph }G\text{ whose edges have distinct weights. } \\\\
2 &  \textbf{Output. } \text{The minimum spanning forest of }G .  \\\\
3 &  \textbf{Method. }  \\\\
4 & \text{Initialize a forest }F\text{ to be a set of one-vertex trees} \\\\
5 &  \textbf{while } \text{True} \\\\
6 &  \qquad \text{Find the components of }F\text{ and label each vertex of }G\text{ by its component } \\\\
7 &  \qquad \text{Initialize the cheapest edge for each component to "None"} \\\\
8 &  \qquad  \textbf{for } \text{each edge }(u, v)\text{ of }G  \\\\
9 &  \qquad\qquad  \textbf{if }  u\text{ and }v\text{ have different component labels} \\\\
\end{array}
$$

---

$$
\begin{array}{ll}
10 &  \qquad\qquad\qquad  \textbf{if }  (u, v)\text{ is cheaper than the cheapest edge for the component of }u  \\\\
11 &  \qquad\qquad\qquad\qquad\text{ Set }(u, v)\text{ as the cheapest edge for the component of }u \\\\
12 &  \qquad\qquad\qquad  \textbf{if }  (u, v)\text{ is cheaper than the cheapest edge for the component of }v  \\\\
13 &  \qquad\qquad\qquad\qquad\text{ Set }(u, v)\text{ as the cheapest edge for the component of }v  \\\\
14 &  \qquad  \textbf{if }\text{ all components'cheapest edges are "None"} \\\\
15 &  \qquad\qquad  \textbf{return }  F \\\\
16 &  \qquad  \textbf{for }\text{ each component whose cheapest edge is not "None"} \\\\
17 &  \qquad\qquad\text{ Add its cheapest edge to }F \\\\
\end{array}
$$

需要注意边与边的比较通常需要第二关键字（例如按编号排序），以便当边权相同时分出边的大小。

---

## 习题

-   [「HAOI2006」聪明的猴子](https://www.luogu.com.cn/problem/P2504)
-   [「SCOI2005」繁忙的都市](https://loj.ac/problem/2149)

---

## 最小生成树的唯一性

考虑最小生成树的唯一性。如果一条边 **不在最小生成树的边集中**，并且可以替换与其 **权值相同、并且在最小生成树边集** 的另一条边。那么，这个最小生成树就是不唯一的。

对于 Kruskal 算法，只要计算为当前权值的边可以放几条，实际放了几条，如果这两个值不一样，那么就说明这几条边与之前的边产生了一个环（这个环中至少有两条当前权值的边，否则根据并查集，这条边是不能放的），即最小生成树不唯一。

寻找权值与当前边相同的边，我们只需要记录头尾指针，用单调队列即可在 $O(\alpha(m))$（m 为边数）的时间复杂度里优秀解决这个问题（基本与原算法时间相同）。

---

" 例题：[POJ 1679](http://poj.org/problem?id=1679)"
```cpp
#include <algorithm>
#include <cstdio>

struct Edge {
  int x, y, z;
};

int f[100001];
Edge a[100001];

int cmp(const Edge& a, const Edge& b) { return a.z < b.z; }

int find(int x) { return f[x] == x ? x : f[x] = find(f[x]); }

int main() {
  int t;
  scanf("%d", &t);
  while (t--) {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) f[i] = i;
    for (int i = 1; i <= m; i++) scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].z);
    std::sort(a + 1, a + m + 1, cmp);  // 先排序
    int num = 0, ans = 0, tail = 0, sum1 = 0, sum2 = 0;
    bool flag = 1;
    for (int i = 1; i <= m + 1; i++) {  // 再并查集加边
      if (i > tail) {
        if (sum1 != sum2) {
          flag = 0;
          break;
        }
        sum1 = 0;
        for (int j = i; j <= m + 1; j++) {
          if (a[j].z != a[i].z) {
            tail = j - 1;
            break;
          }
          if (find(a[j].x) != find(a[j].y)) ++sum1;
        }
        sum2 = 0;
      }
      if (i > m) break;
      int x = find(a[i].x);
      int y = find(a[i].y);
      if (x != y && num != n - 1) {
        sum2++;
        num++;
        f[x] = f[y];
        ans += a[i].z;
      }
    }
    if (flag)
      printf("%d\n", ans);
    else
      printf("Not Unique!\n");
  }
  return 0;
}

```